PageRank通過網路浩瀚的超連結來往來確定一個頁面的等級。 Google把從A頁面到B頁面的連結解釋為A頁面給B頁面投票 Google根據投票來源(甚至來源的來源,即連結到A頁面的頁面)和投票目標的等級來決定新的等級,簡單的說,一個高等級的頁面可以使其他低等級頁面的等級提升。
PageRank演算法
PageRank讓連結來"投票"
一個頁面的"得票數"由所有鏈向它的頁面的重要性決定。到一個頁面的超連結相當於對該頁投一票。一個頁面的PageRank是由所有鏈向它的頁面("鏈入頁面")的重要性經過遞歸演算法得到的。一個有很多鏈入的頁面會有很高的等級,相反如果一個頁面沒有任何鏈入頁面,那麼它沒有等級。2005年初,Google為網頁連結推出一項新屬性"nofollow",令網站管理員和網誌作者可以做出一些Google不會跟蹤的連結;這些連結不算作"投票". nofollow的設置可以抵制評論垃圾。
Google工具條上的PageRank從0到10. 它似乎是一個對數標度演算法。這個演算法的細節是未知的。PageRank是Google的商標. 這個名字是否與Google創始人拉里·佩奇(Page從此而來)有關,又或者只是巧合,仍然是個謎。 PageRank技術已經申請專利。
PageRank演算法中的點擊演算法是由Jon Kleinberg提出的.
PageRank演算法
簡單的假設一個由4個頁面組成的小團體:A, B, C 和 D.如果所有頁面都鏈向A,那麼A的PR (PageRank)值將是B, C and D的和.
- PR(A) = PR(B) + PR(C) + PR(D)
繼續假設B也有連結到C, 並且D也有連結到包括A的3個頁面。一個頁面不能投票2次。所以B給每個頁面半票. 以同樣的邏輯,D投出的票只有三分之一算到了A的PageRank上.
換句話說,根據鏈處總數平分一個頁面的PR值.
最後,所有這些被換算為一個百分比再乘上一個係數q。由於下面的演算法,沒有頁面的PageRank會是0. 所以,Google通過數學系統給了每個頁面一個最小值1 − q.
所以一個頁面的PageRank是由其他頁面的PageRank計算得到. Google不斷的重複計算每個頁面的PageRank. 如果您給每個頁面一個隨機PageRank值(非0),那麼經過不斷的重複計算,這些頁面的PR值會趨向於正常和穩定。 這就是搜索引擎使用它的原因。
完整的
這個方程式引入了隨機瀏覽的概念,即有人上網無聊隨機打開一些頁面,點一些連結。一個頁面的PageRank值也影響了它被隨機瀏覽的機率。為了便於理解,這裡假設上網者不斷點網頁上的連結,最終到了一個沒有任何鏈出頁面的網頁,這時候上網者會隨機到另外的網頁開始瀏覽。
為了對那些有鏈出的頁面公平,q = 0.15(q的意義見上文)的演算法被用到了所有頁面上, 估算頁面可能被上網者放入書籤的機率。
所以,這個等式如下:
p1,p2,...,pN是被研究的頁面, M(pi)是鏈入pi頁面的數量, L(pj)是pj鏈出頁面的數量, 而N是所有頁面的數量。
PageRank值是一個特殊矩陣中的特徵向量。這個特徵向量為
R是等式的答案
如果pj不鏈向pi, 而且對每個j都成立時,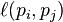 等於0
等於0
這項技術主要的弊端是,舊的頁面等級會比新頁面高,因為新頁面,即使是非常好的頁面,也不會有很多連結,除非他是一個站點的子站點。
這就是PageRank需要多項演算法結合的原因。PageRank似乎傾向於維基百科頁面,在條目名稱的搜索結果中總在大多數或者其他所有頁面之前。原因主要是維基百科內相互的連結很多,並且有很多站點鏈入。
Google經常處罰惡意提高PageRank的行為。Google究竟怎樣區分正常的連結交換和不正常的連結堆積仍然是商業機密。
「PageRank」的文獻信息
文章名稱:PageRank
作者:維基百科編者
出版社:維基百科,
最後更新日期:2007年01月8日16:41(協調世界時)
引用日期:2007年01月29日23:49(協調世界時)
永久連結:http://zh.wikipedia.org/w/index.php?title=PageRank&oldid=3288831
文章版本編號:3288831
以下是幾種常用的參考文獻格式,請確保格式符合您的需求。
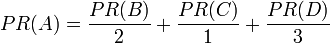
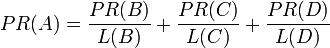
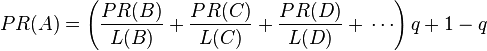
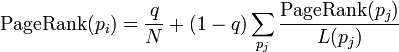

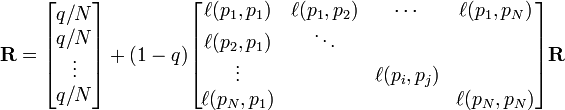
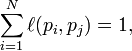
第四色成人電影
回覆刪除第一色成人影院
第一色成人網站
第四色26uuu成人網
第四色成人影院圖片
大香蕉在線影院
第四色在線影院
成人依依網狠狠射
依依成人射
成人依依網電影
你懂的快播電影導航
美女色影院
美女色影院在線
美女色影視
男色女色成人網
男色女色網酒色網
女色網網址
男色天下圖片
18不禁女色
丁香女色網五月
閃閃電影院
日本女色電影
女色電影網
很黃很色的動態圖
色動態圖
性之圖吧性之色魚
哥要搞中文網
哥也射中文網
夜必擼影院
哥也愛去中文網
哥去愛娛樂中文網哥
哥去射中文網
哥要搞中文網
色欲影視性慾
大漠綜合網
來吧綜合網亞洲電影
m6mm美眉娛樂大聯盟
免費言情小說閱讀網
360小說免費閱讀網
飛盧免費小說閱讀網
愛搜藏影視中心
hiav激色影城
361快播理論電影
女女性行為視頻
女性成人玩具用法
女性成人玩具用法心得
男成人玩具用品的用法
女性器具的用法圖片
女女性行為圖片
哥哥成人電影網